Mudanças entre as edições de "Projeto Apostol"
m |
|||
| Linha 6: | Linha 6: | ||
* Coloque o enunciado (em inglês?). | * Coloque o enunciado (em inglês?). | ||
* Resolva-o o mais detalhada e claramente possível (em português?), fazendo comentários e referências úteis. | * Resolva-o o mais detalhada e claramente possível (em português?), fazendo comentários e referências úteis. | ||
| − | * Use [[ | + | * Use [[LaTeX]] para notações matemáticas. |
== Prefácio == | == Prefácio == | ||
Edição atual tal como às 19h49min de 22 de fevereiro de 2012
O Projeto Apostol tem como objetivo reunir a resolução detalhada e comentada dos exercícios dos volumes I e II do Apostol.
Índice
Intruções Gerais
- Escolha um exercício qualquer de sua opção.
- Coloque o enunciado (em inglês?).
- Resolva-o o mais detalhada e claramente possível (em português?), fazendo comentários e referências úteis.
- Use LaTeX para notações matemáticas.
Prefácio
Estratégias de resolução
Manual de sobrevivência na Selva
- Deriva. Não deu?
- Deriva de novo. Não deu?
- Faz por indução. Não deu?
- Prova por absurdo.
Apostol Vol. I
I - Part 1. Historical Introduction
I 1.4 Exercises
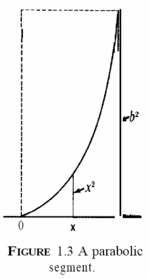
1. (a) Modify the region in Figure 1.3 by assuming that the ordinate at each Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2x^2} instead of Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2} . Draw the new figure. Check through the principal steps in the foregoing section and find what effect this has on the calculation of the area.
Do the same if the cordinate at each Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is
(b) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3x^2}
(c) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}x^2}
(d) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2x^2 + 1}
(e) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax^2 + c}
Resolução:
Apostol Vol. II
1. Linear Spaces
1.5 Exercises
In Exercises 1 through 28, determine whether each of the given sets is a real linear space, if addition and multiplication by real scalars are defined in the usual way. For those that are not, tell which axioms fail to hold. The functions in Exercises 1 through 17 are real-valued. In Exercises 3, 4, and 5, each function has domain containing 0 and 1. In Exercises 7 through 12, each domain contains all real numbers.
1. All rational functions.
2. All rational functions Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{f}{g}} , with the degree of Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f \le} the degree of Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} (including Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = 0} ).
3. All f with Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(0) = f(1)} .
4. All f with Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2f(0) = f(1)} .
5. All f with Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(1)= 1 + f(0)} .
6. All step functions defined on Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,1]} .
7. All Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\mbox{ with }f(x) \to 0} as Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \to \infty} .
8. All even functions.
9. All odd functions.
10. All bounded functions.
11. All increasing functions.
12. All functions with period 2a.
13. All f integrable on Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0, 1]} with Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{1} f(x) dx = 0} .
14. All f integrable on Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0, 1]} with Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{0}^{1} f(x) dx \ge 0} .
15. All f satisfying Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = f(1 - x)} for all x.
16. All Taylor polynomials of degree Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \le n} for a fixed n (including the zero polynomial).
17. All solutions of a linear second-order homogeneous differential equation Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y'' + P(x)y' + Q(x)y = 0} , where P and Q are given functions, continuous everywhere.
18. All bounded real sequences.
19. All convergent real sequences.
20. All convergent real series.
21. All absolutely convergent real series.
22. All vectors (x, y, z) in V, with z = 0.
23. All vectors (x, y, z) in V, with x = 0 or y = 0.
24. All vectors (x, y, z) in V, with y = 5x.
25. All vectors (x, y, z) in V, with 3x + 4y = 1, z = 0.
26. All vectors (x, y, z) in V, which are scalar multiples of (1, 2, 3).
27. All vectors (x, y, z) in V, whose components satisfy a system of three linear equations of the form :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{1,1}x + a_{1,2}y + a_{1,3}z = 0, \quad a_{2,1}x + a_{2,2}y + a_{2,3}z = 0 , \quad a_{3,1}x + a_{3,2}y + a_{3,3} = 0.}
28. All vectors in Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_n} that are linear combinations of two given vectors A and B.
Resolução:
Recordando os axiomas de um espaço linear (segundo o Apostol):
A1. Axioma 1: Fechamento sob adição: Para todo par de elementos x e y em V, corresponde um único elemento em V chamado a soma de x e y, denotado por x + y.
A2. Axioma 2: Fechamento sob multiplicação por números reais: Para todo x em V e todo número real a, corresponde um elemento em V chamado o produto de a e x, denotado por ax.
(a ser continuado)
1. Funções racionais são funções do tipo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{P}{Q}} onde P e Q são polinômios. Basta verificar que somando-se duas funções Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{P_1}{Q_1} + \frac{P_2}{Q_2}} , tem-se uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{P_1 Q_2 + P_2 Q_1}{Q_1 Q_2}} , como o produto e a soma de polinômios são também polinômios, a soma é uma função racional que satisfaz A1. Pelas propriedades da soma de polinômios, satisfaz também A3 e A4. Como existe o polinômio nulo e para cada polinômio P, -P é também um polinômio, as funções racionais satisfazem também A5 e A6. As propriedades A2, A7, A8, A9 e A10 seguem-se da multiplicação de um polinômio por um número real, que também é um polinômio, e de A1.